Vector
quantization
offers a flexible way to develop a coarse-grained representation of 3D
biological
data from a variety of biophysical sources. The following figure shows
the
structure of an actin monomer (backbone trace + atoms) encoded by four
so-called codebook vectors :
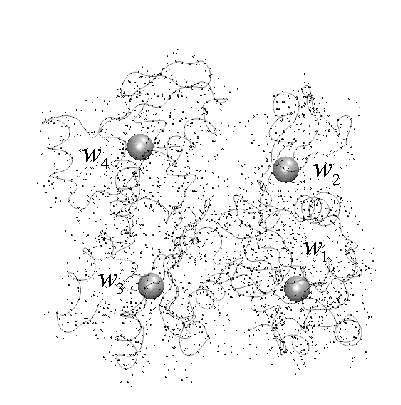Given a certain
number
of vectors, we would like to make sure that the vector positions are
statistically
reliable and reproducible for them to be useful for the registration of
the encoded features (Wriggers et al, 1998).
Therefore, we employ two quantization algorithms
with
different characteristics, the topology-representing neural network
(TRN),
and the Linde-Buzo-Gray (LBG, also called k
-means) algorithms. TRN performs a global stochastic search using
random
start vectors. A number of statistically independent TRN runs is
repeated
and the results are clustered and averaged. TRN is useful if vector
positions are determined the first time. On the other hand, LBG
performs only a single run of local gradient descent search. It is
useful if one wants to update existing vector positions, or if one
wants to add distance constraints (see below).
It can be shown
that both LBG and TRN minimize the so-called distortion error
of the discrete representation. In signal processing this error
measures the fidelity of the
data encoding (the original use of vector quantization was in data
compression). In our case the error is defined as the mean-squares
deviation of the discrete set of vectors from the corresponding
(encoded) 3D data. LBG finds only
the nearest local minimum of the error, and is therefore unreliable for
global searches. TRN with it's stochastic (Monte Carlo) approach comes
close to finding
the global minimum. The TRN search can be improved even more by a
clustering
of vector positions from a number of statistically independent runs.
The
clustering yields average positions of vectors and their statistical
variabilities.
The statistical variabilities are very small compared to the typical
size
of proteins.
Ideally, if one
could find the global minimum of the error exactly, the vector
distribution is fully
determined by the input density distribution. In this situation the
codebook
vectors form a set of "control points" or "landmarks" that provide
information
about the shape and density distribution of a 3D biological object,
similar
to the control points that determine the shape of Bézier spline
curves
in computer graphics. Therefore, the TRN algorithm presents a good
choice
for learning the characteristics of 3D biological datasets at reduced
complexity.
The LBG algorithm can then be used to build upon existing vector
positions.
In rigid-body
docking (Birmanns and Wriggers, 2007), vector
quantization is used to discretize both high- and
low-resolution data sets. Pairs of corresponding codebook vectors are
then identified and superimposed by a least-squares fit. The codebook
vector least-squares fit results in a
superposition of the corresponding high- and low-resolution data sets:
This approach is
particularly useful also in situations where there are conformational
changes that require flexible fitting. The codebook vectors can be used
as constraints for the fitting using molecular dynamics simulation
tools. The colored regions in the following diagram are the so-called
Voronoi (nearest neighbor) cells whose
centroids should coincide with the generating vectors:
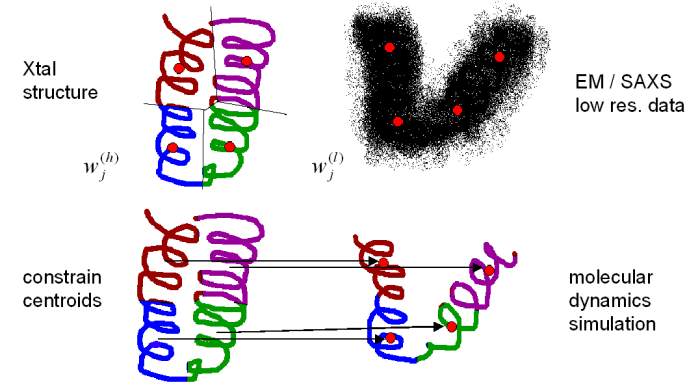
Fitting of the
centroids to the low-resolution vector positions induces the desired
conformational change. If one is concerned about the stereochemical
quality of the fitting, it is possible to constrain the distances
between the vectors to reduce the effect of noise and experimental
limitations on the vector positions:
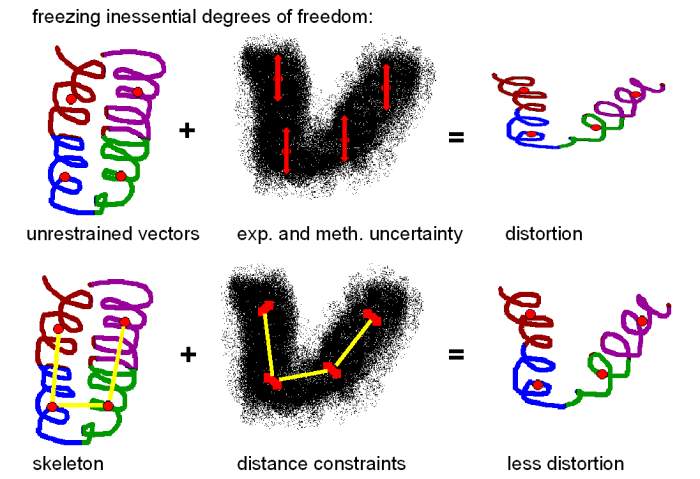
This "skeleton"
based approach is related to 3D motion
capture technology used in the entertainment industry and in
biomechanics. The
implementation of the constraints requires that the vector positions
are
updated incrementally. This is accomplished by using the LBG algorithm
instead
of TRN. To get by with only a local LBG optimization, a global search
with
the stochastic TRN method should be applied first in the absence of
constraints.
The TRN vectors (and the constraints) are then used as input parameters
for
the subsequent LBG refinement. The constraints are enforced with the
iterative
SHAKE algorithm (see Wriggers and Chacon, 2001).
|
